Tasks Details
hard
Given a set of points on a cartesian plane, find the minimum distance between some pair of them to maximise another metric.
Task Score
50%
Correctness
100%
Performance
12%
There are N sheep relaxing in a field. They are positioned at points with integer coordinates. Each sheep has a square sunshade, so as not to overheat. The sunshade of a sheep standing at position (X, Y) spreads out to a distance of D from (X, Y), covering a square whose middle is at (X, Y) and whose sides are of length 2D. More precisely, it covers a square with vertices in points (X − D, Y − D), (X − D, Y + D), (X + D, Y − D) and (X + D, Y + D). Sheep are in the centres of their sunshades. Sunshades edges are parallel to the coordinate axes.
Every sheep spreads out its sunshade to the same width. No two sunshades can overlap, but their borders can touch.
What is the maximum integer width D to which the sheep can spread out their sunshades?
Write a function:
def solution(X, Y)
that, given two arrays X and Y of length N denoting the positions of the sheep, returns the maximum value of D to which the sheep can spread out their sunshades. There are at least two sheep in the flock, and no two sheep share a point with the same coordinates.
Examples:
1. Given X=[0, 0, 10, 10] and Y=[0, 10, 0, 10],
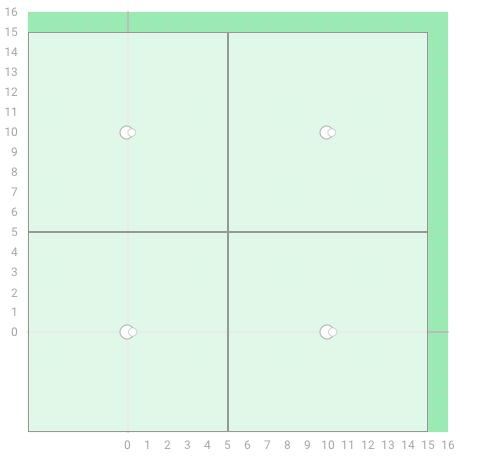
the function should return 5.
2. Given X=[1, 1, 8] and Y=[1, 6, 0],
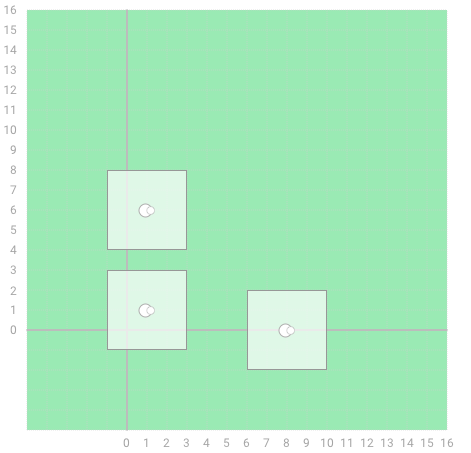
the function should return 2.
Write an efficient algorithm for the following assumptions:
- N is an integer within the range [2..100,000];
- each element of arrays X and Y is an integer within the range [0..100,000];
- no two sheep are standing in the same position.
Copyright 2009–2025 by Codility Limited. All Rights Reserved. Unauthorized copying, publication or disclosure prohibited.
Solution
Programming language used Python
Time spent on task 1 minutes
Notes
not defined yet
Code: 09:44:18 UTC,
java,
autosave
Code: 09:44:32 UTC,
py,
autosave
# you can write to stdout for debugging purposes, e.g.
# print("this is a debug message")
import math
def distance(point1,point2):
d = math.sqrt((point1[0]-point2[0])**2 + (point1[1]-point2[1])**2)
return d
def points(X,Y):
pointsList = []
for i in range(0,len(X)):
pointsList.append([X[i],Y[i]])
return pointsList
def min_distance(points):
if len(points) ==2:
return [(points[0],points[1])]
else:
twoPoints = {}
for i in range(0, len(points)-1):
for j in range(i+1,len(points)):
d = distance(points[i], points[j])
twoPoints.update({(i,j):d})
min_d = min(twoPoints.values())
indexPair = [key for key in twoPoints.keys() if twoPoints.get(key) == min_d or twoPoints.get(key) <= min_d*math.sqrt(2) ]
pointsPair = [(points[index[0]],points[index[1]]) for index in indexPair ]
return pointsPair
def solution(X, Y):
# write your code in Python 3.6
p = points(X,Y)
pointsPairs = min_distance(p)
min_determinate = 100000
for pair in pointsPairs:
p1,p2 = pair[0],pair[1]
dx = abs(p1[0]-p2[0])
dy = abs(p1[1]-p2[1])
determinate = max(dx,dy)
if determinate <= min_determinate:
min_determinate = determinate
D = int(min_determinate/2)
return D
Code: 09:44:36 UTC,
py,
verify,
result: Passed
# you can write to stdout for debugging purposes, e.g.
# print("this is a debug message")
import math
def distance(point1,point2):
d = math.sqrt((point1[0]-point2[0])**2 + (point1[1]-point2[1])**2)
return d
def points(X,Y):
pointsList = []
for i in range(0,len(X)):
pointsList.append([X[i],Y[i]])
return pointsList
def min_distance(points):
if len(points) ==2:
return [(points[0],points[1])]
else:
twoPoints = {}
for i in range(0, len(points)-1):
for j in range(i+1,len(points)):
d = distance(points[i], points[j])
twoPoints.update({(i,j):d})
min_d = min(twoPoints.values())
indexPair = [key for key in twoPoints.keys() if twoPoints.get(key) == min_d or twoPoints.get(key) <= min_d*math.sqrt(2) ]
pointsPair = [(points[index[0]],points[index[1]]) for index in indexPair ]
return pointsPair
def solution(X, Y):
# write your code in Python 3.6
p = points(X,Y)
pointsPairs = min_distance(p)
min_determinate = 100000
for pair in pointsPairs:
p1,p2 = pair[0],pair[1]
dx = abs(p1[0]-p2[0])
dy = abs(p1[1]-p2[1])
determinate = max(dx,dy)
if determinate <= min_determinate:
min_determinate = determinate
D = int(min_determinate/2)
return D
Analysis
Code: 09:44:41 UTC,
py,
verify,
result: Passed
# you can write to stdout for debugging purposes, e.g.
# print("this is a debug message")
import math
def distance(point1,point2):
d = math.sqrt((point1[0]-point2[0])**2 + (point1[1]-point2[1])**2)
return d
def points(X,Y):
pointsList = []
for i in range(0,len(X)):
pointsList.append([X[i],Y[i]])
return pointsList
def min_distance(points):
if len(points) ==2:
return [(points[0],points[1])]
else:
twoPoints = {}
for i in range(0, len(points)-1):
for j in range(i+1,len(points)):
d = distance(points[i], points[j])
twoPoints.update({(i,j):d})
min_d = min(twoPoints.values())
indexPair = [key for key in twoPoints.keys() if twoPoints.get(key) == min_d or twoPoints.get(key) <= min_d*math.sqrt(2) ]
pointsPair = [(points[index[0]],points[index[1]]) for index in indexPair ]
return pointsPair
def solution(X, Y):
# write your code in Python 3.6
p = points(X,Y)
pointsPairs = min_distance(p)
min_determinate = 100000
for pair in pointsPairs:
p1,p2 = pair[0],pair[1]
dx = abs(p1[0]-p2[0])
dy = abs(p1[1]-p2[1])
determinate = max(dx,dy)
if determinate <= min_determinate:
min_determinate = determinate
D = int(min_determinate/2)
return D
Analysis
Code: 09:44:43 UTC,
py,
final,
score:
50
# you can write to stdout for debugging purposes, e.g.
# print("this is a debug message")
import math
def distance(point1,point2):
d = math.sqrt((point1[0]-point2[0])**2 + (point1[1]-point2[1])**2)
return d
def points(X,Y):
pointsList = []
for i in range(0,len(X)):
pointsList.append([X[i],Y[i]])
return pointsList
def min_distance(points):
if len(points) ==2:
return [(points[0],points[1])]
else:
twoPoints = {}
for i in range(0, len(points)-1):
for j in range(i+1,len(points)):
d = distance(points[i], points[j])
twoPoints.update({(i,j):d})
min_d = min(twoPoints.values())
indexPair = [key for key in twoPoints.keys() if twoPoints.get(key) == min_d or twoPoints.get(key) <= min_d*math.sqrt(2) ]
pointsPair = [(points[index[0]],points[index[1]]) for index in indexPair ]
return pointsPair
def solution(X, Y):
# write your code in Python 3.6
p = points(X,Y)
pointsPairs = min_distance(p)
min_determinate = 100000
for pair in pointsPairs:
p1,p2 = pair[0],pair[1]
dx = abs(p1[0]-p2[0])
dy = abs(p1[1]-p2[1])
determinate = max(dx,dy)
if determinate <= min_determinate:
min_determinate = determinate
D = int(min_determinate/2)
return DAnalysis summary
The following issues have been detected: timeout errors.
Analysis
Detected time complexity:
O(N**2)
expand all
Correctness tests
1.
0.036 s
OK
2.
0.036 s
OK
3.
0.036 s
OK
1.
0.040 s
OK
2.
0.040 s
OK
1.
0.040 s
OK
2.
0.040 s
OK
1.
0.040 s
OK
2.
0.040 s
OK
1.
0.040 s
OK
2.
0.040 s
OK
1.
0.048 s
OK
expand all
Performance tests
1.
0.036 s
OK
2.
0.036 s
OK
3.
0.036 s
OK
4.
0.036 s
OK
5.
0.036 s
OK
1.
12.824 s
TIMEOUT ERROR,
running time: 12.82 sec., time limit: 10.50 sec.
stderr:
Traceback (most recent call last):
File "exec.py", line 139, in <module>
main()
File "exec.py", line 101, in main
result = solution( X, Y )
File "/tmp/solution.py", line 35, in solution
pointsPairs = min_distance(p)
File "/tmp/solution.py", line 25, in min_distance
twoPoints.update({(i,j):d})
MemoryError
big_line
Points are arranges in a line.
Points are arranges in a line.
✘
TIMEOUT ERROR
running time: >10.00 sec., time limit: 4.75 sec.
running time: >10.00 sec., time limit: 4.75 sec.
1.
10.000 s
TIMEOUT ERROR,
running time: >10.00 sec., time limit: 4.75 sec.
2.
8.000 s
TIMEOUT ERROR,
running time: >8.00 sec., time limit: 2.02 sec.
big_grid
Points are arranged in a grid. X3 points
Points are arranged in a grid. X3 points
✘
TIMEOUT ERROR
running time: 1.23 sec., time limit: 0.29 sec.
running time: 1.23 sec., time limit: 0.29 sec.
1.
1.232 s
TIMEOUT ERROR,
running time: 1.23 sec., time limit: 0.29 sec.
2.
12.924 s
TIMEOUT ERROR,
running time: 12.92 sec., time limit: 9.36 sec.
stderr:
Traceback (most recent call last):
File "exec.py", line 139, in <module>
main()
File "exec.py", line 101, in main
result = solution( X, Y )
File "/tmp/solution.py", line 35, in solution
pointsPairs = min_distance(p)
File "/tmp/solution.py", line 25, in min_distance
twoPoints.update({(i,j):d})
MemoryError
big_againts_greedy
Tests against random and greedy solutions.
Tests against random and greedy solutions.
✘
TIMEOUT ERROR
running time: >10.00 sec., time limit: 4.85 sec.
running time: >10.00 sec., time limit: 4.85 sec.
1.
10.000 s
TIMEOUT ERROR,
running time: >10.00 sec., time limit: 4.85 sec.
2.
7.000 s
TIMEOUT ERROR,
running time: >7.00 sec., time limit: 1.36 sec.
3.
6.000 s
TIMEOUT ERROR,
running time: >6.00 sec., time limit: 0.48 sec.
big_square
Points are arranged in a square.
Points are arranged in a square.
✘
TIMEOUT ERROR
running time: 12.53 sec., time limit: 9.57 sec.
running time: 12.53 sec., time limit: 9.57 sec.
1.
12.532 s
TIMEOUT ERROR,
running time: 12.53 sec., time limit: 9.57 sec.
stderr:
Traceback (most recent call last):
File "exec.py", line 139, in <module>
main()
File "exec.py", line 101, in main
result = solution( X, Y )
File "/tmp/solution.py", line 35, in solution
pointsPairs = min_distance(p)
File "/tmp/solution.py", line 25, in min_distance
twoPoints.update({(i,j):d})
MemoryError