Test results - Codility

Tasks Details

medium

1. DividingTheKingdom

In how many ways can you split a kingdom into two parts, so that the parts contain equal number of gold mines?

Task Score

100%

Correctness

100%

Performance

100%

An old king wants to divide his kingdom between his two sons. He is well known for his justness and wisdom, and he plans to make a good use of both of these attributes while dividing his kingdom.

The kingdom is administratively split into square boroughs that form an N × M grid. Some of the boroughs contain gold mines. The king knows that his sons do not care as much about the land as they do about gold, so he wants both parts of the kingdom to contain exactly the same number of mines. Moreover, he wants to split the kingdom with either a horizontal or a vertical line that goes along the borders of the boroughs (splitting no borough into two parts).

The goal is to count how many ways he can split the kingdom.

Write a function:

class Solution { public int solution(int N, int M, int[] X, int[] Y); }

that, given two arrays of K integers X and Y, denoting coordinates of boroughs containing the gold mines, will compute the number of fair divisions of the kingdom.

For example, given N = 5, M = 5, X = [0, 4, 2, 0] and Y = [0, 0, 1, 4], the function should return 3. The king can divide his land in three different ways shown on the picture below.

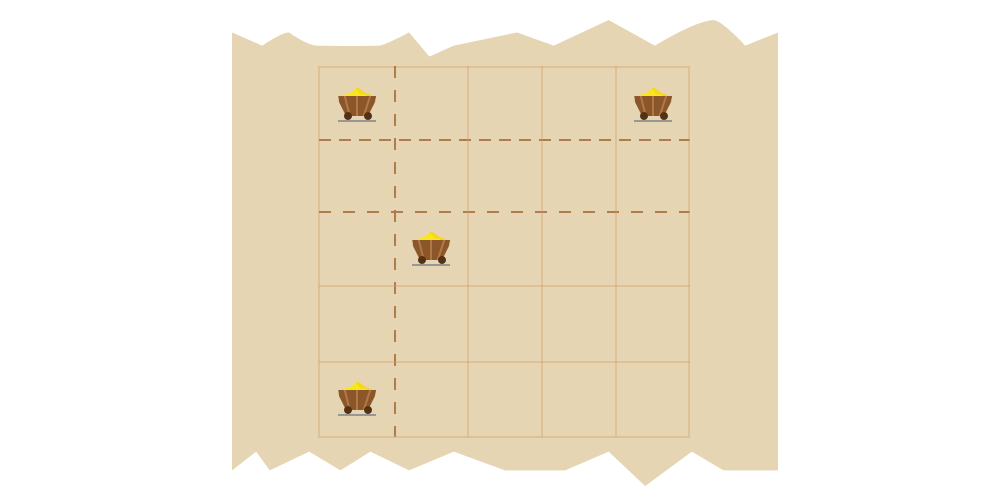
Divide horizontally in two ways or vertically in one way

Write an efficient algorithm for the following assumptions:

N and M are integers within the range [1..100,000];

K is an integer within the range [1..100,000];

each element of array X is an integer within the range [0..N-1];

each element of array Y is an integer within the range [0..M-1].

Solution

Programming language used Java 21

Time spent on task 1 minutes

Notes

not defined yet

Code: 01:28:03 UTC, java, autosave

show code in pop-up

1 2 3 4 5 6 7 8 9 10 11

// you can also use imports, for example:
// import java.util.*;

// you can write to stdout for debugging purposes, e.g.
// System.out.println("this is a debug message");

class Solution {
    public int solution(int N, int M, int[] X, int[] Y) {
        // write your code in Java SE 8
    }
}

Code: 01:28:23 UTC, java, autosave

show code in pop-up

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57

// you can also use imports, for example:
// import java.util.*;

// you can write to stdout for debugging purposes, e.g.
// System.out.println("this is a debug message");

class Solution {
    private int[] xList;
    private int[] yList;
    private int half = 0;
    
    public int solution(int N, int M, int[] X, int[] Y) {
        // not too sure with odd number cases
        if (X.length % 2 != 0)
            System.out.println("not an even number");
            
        // setup
        this.half = X.length / 2;
        if (half == 0)
            return 0;
        int ways = 0;
        xList = count(xList, X, N);
        yList = count(yList, Y, M);
        
        // I could break the loop if more than half in one area, but no need in terms of big O
        for (int x = 1; x < N; x++) {
            if (xAreaContainsHalf(x))
                ways++;
        }
        for (int y = 1; y < M; y++) {
            if (yAreaContainsHalf(y))
                ways++;
        }
        return ways;
    }
    
    private boolean xAreaContainsHalf(int x) {
        return xList[x - 1] == half;
    }
    
    private boolean yAreaContainsHalf(int y) {
        return yList[y - 1] == half;
    }
    
    private int[] count(int[] list, int[] nums, int max) {
        list = new int[max];
        for (int i = 0; i < nums.length; i++) {
            list[nums[i]]++;
        }
        int acc = 0;
        for (int i = 0; i < list.length; i++) {
            list[i] += acc;
            acc = list[i];
        }
        return list;
    }
}

Code: 01:28:33 UTC, java, autosave

show code in pop-up

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57

// you can also use imports, for example:
// import java.util.*;

// you can write to stdout for debugging purposes, e.g.
// System.out.println("this is a debug message");

class Solution {
    private int[] xList;
    private int[] yList;
    private int half = 0;
    
    public int solution(int N, int M, int[] X, int[] Y) {
        // not too sure with odd number cases
        if (X.length % 2 != 0)
            return 0;
            
        // setup
        this.half = X.length / 2;
        if (half == 0)
            return 0;
        int ways = 0;
        xList = count(xList, X, N);
        yList = count(yList, Y, M);
        
        // I could break the loop if more than half in one area, but no need in terms of big O
        for (int x = 1; x < N; x++) {
            if (xAreaContainsHalf(x))
                ways++;
        }
        for (int y = 1; y < M; y++) {
            if (yAreaContainsHalf(y))
                ways++;
        }
        return ways;
    }
    
    private boolean xAreaContainsHalf(int x) {
        return xList[x - 1] == half;
    }
    
    private boolean yAreaContainsHalf(int y) {
        return yList[y - 1] == half;
    }
    
    private int[] count(int[] list, int[] nums, int max) {
        list = new int[max];
        for (int i = 0; i < nums.length; i++) {
            list[nums[i]]++;
        }
        int acc = 0;
        for (int i = 0; i < list.length; i++) {
            list[i] += acc;
            acc = list[i];
        }
        return list;
    }
}

Code: 01:28:41 UTC, java, verify, result: Passed

show code in pop-up

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55

// you can also use imports, for example:
// import java.util.*;

// you can write to stdout for debugging purposes, e.g.
// System.out.println("this is a debug message");

class Solution {
    private int[] xList;
    private int[] yList;
    private int half = 0;
    
    public int solution(int N, int M, int[] X, int[] Y) {
        // not too sure with odd number cases
        if (X.length % 2 != 0)
            return 0;
            
        // setup
        this.half = X.length / 2;
        int ways = 0;
        xList = count(xList, X, N);
        yList = count(yList, Y, M);
        
        // I could break the loop if more than half in one area, but no need in terms of big O
        for (int x = 1; x < N; x++) {
            if (xAreaContainsHalf(x))
                ways++;
        }
        for (int y = 1; y < M; y++) {
            if (yAreaContainsHalf(y))
                ways++;
        }
        return ways;
    }
    
    private boolean xAreaContainsHalf(int x) {
        return xList[x - 1] == half;
    }
    
    private boolean yAreaContainsHalf(int y) {
        return yList[y - 1] == half;
    }
    
    private int[] count(int[] list, int[] nums, int max) {
        list = new int[max];
        for (int i = 0; i < nums.length; i++) {
            list[nums[i]]++;
        }
        int acc = 0;
        for (int i = 0; i < list.length; i++) {
            list[i] += acc;
            acc = list[i];
        }
        return list;
    }
}

Analysis

expand all Example tests

▶

example
example test

✔

0.004 s

Code: 01:28:44 UTC, java, final, score: 100

show code in pop-up

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55

// you can also use imports, for example:
// import java.util.*;

// you can write to stdout for debugging purposes, e.g.
// System.out.println("this is a debug message");

class Solution {
    private int[] xList;
    private int[] yList;
    private int half = 0;
    
    public int solution(int N, int M, int[] X, int[] Y) {
        // not too sure with odd number cases
        if (X.length % 2 != 0)
            return 0;
            
        // setup
        this.half = X.length / 2;
        int ways = 0;
        xList = count(xList, X, N);
        yList = count(yList, Y, M);
        
        // I could break the loop if more than half in one area, but no need in terms of big O
        for (int x = 1; x < N; x++) {
            if (xAreaContainsHalf(x))
                ways++;
        }
        for (int y = 1; y < M; y++) {
            if (yAreaContainsHalf(y))
                ways++;
        }
        return ways;
    }
    
    private boolean xAreaContainsHalf(int x) {
        return xList[x - 1] == half;
    }
    
    private boolean yAreaContainsHalf(int y) {
        return yList[y - 1] == half;
    }
    
    private int[] count(int[] list, int[] nums, int max) {
        list = new int[max];
        for (int i = 0; i < nums.length; i++) {
            list[nums[i]]++;
        }
        int acc = 0;
        for (int i = 0; i < list.length; i++) {
            list[i] += acc;
            acc = list[i];
        }
        return list;
    }
}

Analysis summary

The solution obtained perfect score.

Analysis

Detected time complexity:

O(N+M+K)

expand all Example tests

▶

example
example test

✔

0.004 s

expand all Correctness tests

▶

one_column
simple test with one column

✔

0.004 s

▶

one_row
simple test with one row

✔

0.004 s

0.008 s

0.004 s

▶

simple_mostly_zeroes
simple test with mostly zeroes in array

✔

0.004 s

▶

combinations
multiple runs, all legal sequences of length 3

✔

0.004 s

10.

0.008 s

11.

0.004 s

12.

0.004 s

13.

0.004 s

14.

0.004 s

▶

random_small
small random tests

✔

0.008 s

▶

diagonal_permutation
goldmines lie on diagonal, but are given in random order

✔

0.004 s

expand all Performance tests

▶

random_large
large random tests

✔

0.004 s

0.008 s

0.380 s

▶

random_long
random tests with many rows or many columns

✔

0.016 s

0.092 s

▶

random_square
random tests with many rows and many columns

✔

0.024 s

0.504 s

▶

largest_answer
max test with largest answer

✔

0.028 s