Tasks Details
hard
Given a set of points on a cartesian plane, find the minimum distance between some pair of them to maximise another metric.
Task Score
100%
Correctness
100%
Performance
100%
There are N sheep relaxing in a field. They are positioned at points with integer coordinates. Each sheep has a square sunshade, so as not to overheat. The sunshade of a sheep standing at position (X, Y) spreads out to a distance of D from (X, Y), covering a square whose middle is at (X, Y) and whose sides are of length 2D. More precisely, it covers a square with vertices in points (X − D, Y − D), (X − D, Y + D), (X + D, Y − D) and (X + D, Y + D). Sheep are in the centres of their sunshades. Sunshades edges are parallel to the coordinate axes.
Every sheep spreads out its sunshade to the same width. No two sunshades can overlap, but their borders can touch.
What is the maximum integer width D to which the sheep can spread out their sunshades?
Write a function:
function solution($X, $Y);
that, given two arrays X and Y of length N denoting the positions of the sheep, returns the maximum value of D to which the sheep can spread out their sunshades. There are at least two sheep in the flock, and no two sheep share a point with the same coordinates.
Examples:
1. Given X=[0, 0, 10, 10] and Y=[0, 10, 0, 10],
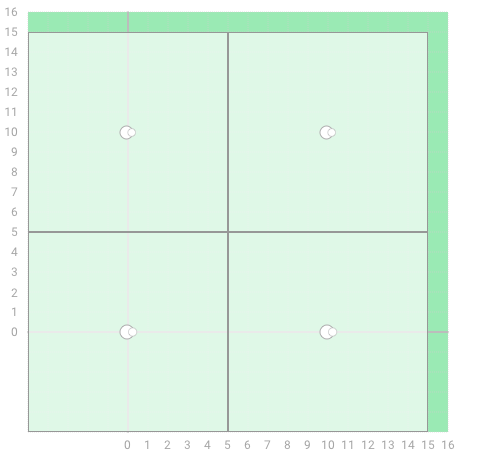
the function should return 5.
2. Given X=[1, 1, 8] and Y=[1, 6, 0],
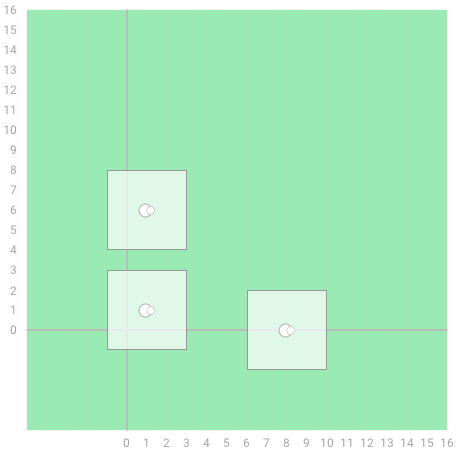
the function should return 2.
Write an efficient algorithm for the following assumptions:
- N is an integer within the range [2..100,000];
- each element of arrays X and Y is an integer within the range [0..100,000];
- no two sheep are standing in the same position.
Copyright 2009–2024 by Codility Limited. All Rights Reserved. Unauthorized copying, publication or disclosure prohibited.
Solution
Programming language used PHP
Total time used 19 minutes
Effective time used 19 minutes
Notes
not defined yet
Task timeline
Code: 12:17:03 UTC,
java,
autosave
Code: 12:17:22 UTC,
php,
autosave
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:18:09 UTC,
php,
verify,
result: Passed
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
User test case 1:
[[0, 6, 5, 6, 2, 4, 2, 4, 7, 6, 2, 8, 6, 2, 0, 8, 0, 5, 3, 6, 2, 5, 1, 3, 0, 1, 5, 0, 2, 8, 4, 5, 8, 0, 3, 7, 8, 7, 1, 5, 2, 3, 3, 1, 3, 6, 8, 5, 6, 4], [3, 2, 2, 10, 8, 6, 10, 3, 5, 8, 7, 10, 5, 9, 8, 5, 7, 6, 2, 7, 5, 5, 3, 7, 6, 10, 10, 2, 4, 7, 4, 3, 6, 9, 8, 4, 4, 8, 5, 4, 2, 6, 10, 2, 3, 3, 9, 9, 9, 9]]
Analysis
Code: 12:19:25 UTC,
php,
verify,
result: Passed
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
User test case 1:
[[0, 6, 5, 6, 2, 4, 2, 4, 7, 6, 2, 8, 6, 2, 0, 8, 0, 5, 3, 6, 2, 5, 1, 3, 0, 1, 5, 0, 2, 8, 4, 5, 8, 0, 3, 7, 8, 7, 1, 5, 2, 3, 3, 1, 3, 6, 8, 5, 6, 4], [3, 2, 2, 10, 8, 6, 10, 3, 5, 8, 7, 10, 5, 9, 8, 5, 7, 6, 2, 7, 5, 5, 3, 7, 6, 10, 10, 2, 4, 7, 4, 3, 6, 9, 8, 4, 4, 8, 5, 4, 2, 6, 10, 2, 3, 3, 9, 9, 9, 9]]
User test case 2:
[[71, 88, 9, 13, 50, 67, 83, 7, 30, 92, 67, 92, 14, 16, 16, 13, 93, 52, 34, 97, 40, 69, 30, 6, 59, 85, 78, 18, 63, 95, 71, 80, 43, 31, 84, 31, 60, 16, 72, 61, 83, 35, 31, 36, 4, 100, 46, 21, 39, 61], [86, 87, 62, 80, 80, 0, 39, 66, 35, 6, 37, 53, 71, 70, 44, 33, 87, 78, 70, 94, 56, 29, 100, 65, 7, 14, 52, 95, 96, 37, 2, 96, 88, 47, 20, 97, 68, 74, 91, 31, 13, 52, 7, 70, 93, 25, 98, 10, 46, 13]]
Analysis
Code: 12:19:44 UTC,
php,
verify,
result: Passed
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
User test case 1:
[[71, 88, 9, 13, 50, 67, 83, 7, 30, 92, 67, 92, 14, 16, 16, 13, 93, 52, 34, 97, 40, 69, 30, 6, 59, 85, 78, 18, 63, 95, 71, 80, 43, 31, 84, 31, 60, 16, 72, 61, 83, 35, 31, 36, 4, 100, 46, 21, 39, 61], [86, 87, 62, 80, 80, 0, 39, 66, 35, 6, 37, 53, 71, 70, 44, 33, 87, 78, 70, 94, 56, 29, 100, 65, 7, 14, 52, 95, 96, 37, 2, 96, 88, 47, 20, 97, 68, 74, 91, 31, 13, 52, 7, 70, 93, 25, 98, 10, 46, 13]]
Analysis
Code: 12:20:01 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:20:21 UTC,
php,
autosave
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1)
$i0=$D[0][0];
$i1=$D[1][0];
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:20:40 UTC,
php,
verify,
result: Passed
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
echo $i0." ".$i1."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
User test case 1:
[[71, 88, 9, 13, 50, 67, 83, 7, 30, 92, 67, 92, 14, 16, 16, 13, 93, 52, 34, 97, 40, 69, 30, 6, 59, 85, 78, 18, 63, 95, 71, 80, 43, 31, 84, 31, 60, 16, 72, 61, 83, 35, 31, 36, 4, 100, 46, 21, 39, 61], [86, 87, 62, 80, 80, 0, 39, 66, 35, 6, 37, 53, 71, 70, 44, 33, 87, 78, 70, 94, 56, 29, 100, 65, 7, 14, 52, 95, 96, 37, 2, 96, 88, 47, 20, 97, 68, 74, 91, 31, 13, 52, 7, 70, 93, 25, 98, 10, 46, 13]]
Analysis
expand all
Example tests
1.
0.004 s
OK
stdout:
0 1
1.
0.004 s
OK
stdout:
0 1
1.
0.004 s
OK
stdout:
0 1
Code: 12:20:55 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
echo $Xi0." ".$i1."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:21:09 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
echo $X[$i0].",".$Y[$i0]." ".$i1."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:21:29 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:21:39 UTC,
php,
verify,
result: Passed
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
User test case 1:
[[71, 88, 9, 13, 50, 67, 83, 7, 30, 92, 67, 92, 14, 16, 16, 13, 93, 52, 34, 97, 40, 69, 30, 6, 59, 85, 78, 18, 63, 95, 71, 80, 43, 31, 84, 31, 60, 16, 72, 61, 83, 35, 31, 36, 4, 100, 46, 21, 39, 61], [86, 87, 62, 80, 80, 0, 39, 66, 35, 6, 37, 53, 71, 70, 44, 33, 87, 78, 70, 94, 56, 29, 100, 65, 7, 14, 52, 95, 96, 37, 2, 96, 88, 47, 20, 97, 68, 74, 91, 31, 13, 52, 7, 70, 93, 25, 98, 10, 46, 13]]
Analysis
expand all
Example tests
1.
0.008 s
OK
stdout:
0,0 2,0
1.
0.008 s
OK
stdout:
0,0 0,10
1.
0.008 s
OK
stdout:
1,1 1,6
Code: 12:22:22 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:22:47 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=0;$i<sizeof($D);$i++)
echo $X[]
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:22:58 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=0;$i<sizeof($D);$i++)
echo $X[$D[$i]]
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:23:10 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=0;$i<sizeof($D);$i++)
echo $X[$D[$i][0]]
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:23:23 UTC,
php,
autosave
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=0;$i<sizeof($D);$i++)
echo $X[$D[$i][0]]." ";
echo "\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:23:30 UTC,
php,
verify,
result: Passed
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=0;$i<sizeof($D);$i++)
echo $X[$D[$i][0]]." ";
echo "\n";
for($i=0;$i<sizeof($D);$i++)
echo $Y[$D[$i][0]]." ";
echo "\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
User test case 1:
[[71, 88, 9, 13, 50, 67, 83, 7, 30, 92, 67, 92, 14, 16, 16, 13, 93, 52, 34, 97, 40, 69, 30, 6, 59, 85, 78, 18, 63, 95, 71, 80, 43, 31, 84, 31, 60, 16, 72, 61, 83, 35, 31, 36, 4, 100, 46, 21, 39, 61], [86, 87, 62, 80, 80, 0, 39, 66, 35, 6, 37, 53, 71, 70, 44, 33, 87, 78, 70, 94, 56, 29, 100, 65, 7, 14, 52, 95, 96, 37, 2, 96, 88, 47, 20, 97, 68, 74, 91, 31, 13, 52, 7, 70, 93, 25, 98, 10, 46, 13]]
Analysis
expand all
Example tests
1.
0.004 s
OK
stdout:
0 2 0 0
1.
0.004 s
OK
stdout:
0 0 10 10 0 10 0 10
1.
0.004 s
OK
stdout:
1 1 8 1 6 0
expand all
User tests
1.
0.004 s
OK
function result: 5
function result: 5
stdout:
21 31 13 30 16 31 59 39 61 9 35 6 7 67 61 40 71 16 14 69 16 67 34 36 13 83 85 84 60 83 92 4 52 78 50 18 43 31 95 100 30 92 46 71 63 72 88 80 93 97 10 7 33 35 44 47 7 46 13 62 52 65 66 0 31 56 2 70 71 29 74 37 70 70 80 13 14 20 68 39 6 93 78 52 80 95 88 97 37 25 100 53 98 86 96 91 87 96 87 94
Code: 12:23:59 UTC,
php,
autosave
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=0;$i<sizeof($D);$i++)
echo $X[$D[$i][0]]." ";
echo "\n";
for($i=0;$i<sizeof($D);$i++)
echo $Y[$D[$i][0]]." ";
echo "\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:24:12 UTC,
php,
verify,
result: Passed
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=0;$i<sizeof($D);$i++)
echo $X[$D[$i][0]]." ";
echo "\n";
for($i=0;$i<sizeof($D);$i++)
echo $Y[$D[$i][0]]." ";
echo "\n";
for($i=0;$i<sizeof($D);$i++)
echo $D[$i][1]." ";
echo "\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
User test case 1:
[[71, 88, 9, 13, 50, 67, 83, 7, 30, 92, 67, 92, 14, 16, 16, 13, 93, 52, 34, 97, 40, 69, 30, 6, 59, 85, 78, 18, 63, 95, 71, 80, 43, 31, 84, 31, 60, 16, 72, 61, 83, 35, 31, 36, 4, 100, 46, 21, 39, 61], [86, 87, 62, 80, 80, 0, 39, 66, 35, 6, 37, 53, 71, 70, 44, 33, 87, 78, 70, 94, 56, 29, 100, 65, 7, 14, 52, 95, 96, 37, 2, 96, 88, 47, 20, 97, 68, 74, 91, 31, 13, 52, 7, 70, 93, 25, 98, 10, 46, 13]]
Analysis
expand all
Example tests
1.
0.008 s
OK
stdout:
0 2 0 0 0 2
1.
0.004 s
OK
stdout:
0 0 10 10 0 10 0 10 0 10 10 14.142135623731
1.
0.004 s
OK
stdout:
1 1 8 1 6 0 1.4142135623731 6.0827625302982 8
expand all
User tests
1.
0.004 s
OK
function result: 5
function result: 5
stdout:
21 31 13 30 16 31 59 39 61 9 35 6 7 67 61 40 71 16 14 69 16 67 34 36 13 83 85 84 60 83 92 4 52 78 50 18 43 31 95 100 30 92 46 71 63 72 88 80 93 97 10 7 33 35 44 47 7 46 13 62 52 65 66 0 31 56 2 70 71 29 74 37 70 70 80 13 14 20 68 39 6 93 78 52 80 95 88 97 37 25 100 53 98 86 96 91 87 96 87 94 23.259406699226 31.780497164141 35.468295701936 46.097722286464 46.818799642879 56.302753041037 59.413803110052 60.307545133258 62.369864518051 62.649820430708 62.681735776859 65.27633568147 66.37017402418 67 68.425141578224 68.818602136341 71.028163428319 71.805292284065 72.367119605523 74.846509604657 75.709972922991 76.53757247261 77.820305833375 78.714674616618 81.049367671809 84.011903918433 86.145226217127 86.348132579692 90.686272390037 91.706052144883 92.195444572929 93.085981758802 93.744333162064 93.744333162064 94.339811320566 96.690227013903 97.943861471764 101.83319694481 101.95096860746 103.07764064044 104.40306508911 106.17438485812 108.25894882179 111.52129841425 114.82595525403 116.03878661896 123.74570699624 124.96399481451 127.34991166075 135.07405376311
Code: 12:25:14 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=0;$i<sizeof($D);$i++)
echo $X[$D[$i][0]].",";
echo "\n";
for($i=0;$i<sizeof($D);$i++)
echo $Y[$D[$i][0]]." ";
echo "\n";
for($i=0;$i<sizeof($D);$i++)
echo $D[$i][1]." ";
echo "\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:25:25 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=0;$i<sizeof($D);$i++)
echo $i.": ".$X[$D[$i][0]].",";
echo "\n";
for($i=0;$i<sizeof($D);$i++)
echo $Y[$D[$i][0]]." ";
echo "\n";
for($i=0;$i<sizeof($D);$i++)
echo $D[$i][1]." ";
echo "\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:25:46 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=0;$i<sizeof($D);$i++)
echo $i.": ".$X[$D[$i][0]].",".$Y[$D[$i][0]]." ".$D[$i][1]];
echo "\n";
for($i=0;$i<sizeof($D);$i++)
echo $Y[$D[$i][0]]." ";
echo "\n";
for($i=0;$i<sizeof($D);$i++)
echo $D[$i][1]." ";
echo "\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:26:02 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=0;$i<sizeof($D);$i++)
echo $i.": ".$X[$D[$i][0]].",".$Y[$D[$i][0]]." ".$D[$i][1];
echo "\n";
for($i=0;$i<sizeof($D);$i++)
echo $Y[$D[$i][0]]." ";
echo "\n";
for($i=0;$i<sizeof($D);$i++)
echo $D[$i][1]." ";
echo "\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:26:15 UTC,
php,
verify,
result: Passed
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=0;$i<sizeof($D);$i++)
echo $i.": ".$X[$D[$i][0]].",".$Y[$D[$i][0]]." ".$D[$i][1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
User test case 1:
[[71, 88, 9, 13, 50, 67, 83, 7, 30, 92, 67, 92, 14, 16, 16, 13, 93, 52, 34, 97, 40, 69, 30, 6, 59, 85, 78, 18, 63, 95, 71, 80, 43, 31, 84, 31, 60, 16, 72, 61, 83, 35, 31, 36, 4, 100, 46, 21, 39, 61], [86, 87, 62, 80, 80, 0, 39, 66, 35, 6, 37, 53, 71, 70, 44, 33, 87, 78, 70, 94, 56, 29, 100, 65, 7, 14, 52, 95, 96, 37, 2, 96, 88, 47, 20, 97, 68, 74, 91, 31, 13, 52, 7, 70, 93, 25, 98, 10, 46, 13]]
Analysis
expand all
Example tests
1.
0.004 s
OK
stdout:
0: 0,0 0 1: 2,0 2
1.
0.004 s
OK
stdout:
0: 0,0 0 1: 0,10 10 2: 10,0 10 3: 10,10 14.142135623731
1.
0.004 s
OK
stdout:
0: 1,1 1.4142135623731 1: 1,6 6.0827625302982 2: 8,0 8
expand all
User tests
1.
0.004 s
OK
function result: 5
function result: 5
stdout:
0: 21,10 23.259406699226 1: 31,7 31.780497164141 2: 13,33 35.468295701936 3: 30,35 46.097722286464 4: 16,44 46.818799642879 5: 31,47 56.302753041037 6: 59,7 59.413803110052 7: 39,46 60.307545133258 8: 61,13 62.369864518051 9: 9,62 62.649820430708 10: 35,52 62.681735776859 11: 6,65 65.27633568147 12: 7,66 66.37017402418 13: 67,0 67 14: 61,31 68.425141578224 15: 40,56 68.818602136341 16: 71,2 71.028163428319 17: 16,70 71.805292284065 18: 14,71 72.367119605523 19: 69,29 74.846509604657 20: 16,74 75.709972922991 21: 67,37 76.53757247261 22: 34,70 77.820305833375 23: 36,70 78.714674616618 24: 13,80 81.049367671809 25: 83,13 84.011903918433 26: 85,14 86.145226217127 27: 84,20 86.348132579692 28: 60,68 90.686272390037 29: 83,39 91.706052144883 30: 92,6 92.195444572929 31: 4,93 93.085981758802 32: 52,78 93.744333162064 33: 78,52 93.744333162064 34: 50,80 94.339811320566 35: 18,95 96.690227013903 36: 43,88 97.943861471764 37: 31,97 101.83319694481 38: 95,37 101.95096860746 39: 100,25 103.07764064044 40: 30,100 104.40306508911 41: 92,53 106.17438485812 42: 46,98 108.25894882179 43: 71,86 111.52129841425 44: 63,96 114.82595525403 45: 72,91 116.03878661896 46: 88,87 123.74570699624 47: 80,96 124.96399481451 48: 93,87 127.34991166075 49: 97,94 135.07405376311
Code: 12:29:09 UTC,
php,
autosave
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=1;$i<sizeof($D);$i++)
echo $i.": ".$X[$D[$i][0]].",".$Y[$D[$i][0]]." ".$D[$i][1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
return $m;
}
Code: 12:29:23 UTC,
php,
autosave
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=1;$i<sizeof($D);$i++)
echo $i.": ".$X[$D[$i][0]].",".$Y[$D[$i][0]]." ".$D[$i][1]."\n";
return $m;
}
Code: 12:29:34 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
for($i=1;$i<sizeof($D);$i++)
{
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
}
return $m;
}
Code: 12:29:53 UTC,
php,
autosave
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
}
return $m;
}
Code: 12:30:09 UTC,
php,
autosave
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$m=(int)max(abs(($X[$i-1]-$X[$i])/2) , abs(($Y[$i-1]-$Y[$i1])/2) );
}
return $m;
}
Code: 12:30:27 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$m2=(int)max(abs(($X[$i-1]-$X[$i])/2) , abs(($Y[$i-1]-$Y[$i])/2) );
if($m2<$m)
$m=$m2;
}
return $m;
}
Code: 12:30:33 UTC,
php,
verify,
result: Passed
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$m2=(int)max(abs(($X[$i-1]-$X[$i])/2) , abs(($Y[$i-1]-$Y[$i])/2) );
if($m2<$m)
$m=$m2;
}
return $m;
}
User test case 1:
[[71, 88, 9, 13, 50, 67, 83, 7, 30, 92, 67, 92, 14, 16, 16, 13, 93, 52, 34, 97, 40, 69, 30, 6, 59, 85, 78, 18, 63, 95, 71, 80, 43, 31, 84, 31, 60, 16, 72, 61, 83, 35, 31, 36, 4, 100, 46, 21, 39, 61], [86, 87, 62, 80, 80, 0, 39, 66, 35, 6, 37, 53, 71, 70, 44, 33, 87, 78, 70, 94, 56, 29, 100, 65, 7, 14, 52, 95, 96, 37, 2, 96, 88, 47, 20, 97, 68, 74, 91, 31, 13, 52, 7, 70, 93, 25, 98, 10, 46, 13]]
Analysis
Code: 12:31:55 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$m2=max(abs(($X[$i-1]-$X[$i])/2) , abs(($Y[$i-1]-$Y[$i])/2) );
if($m2<$m)
$m=$m2;
}
return $m;
}
Code: 12:32:02 UTC,
php,
verify,
result: Passed
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$m2=max((int)abs(($X[$i-1]-$X[$i])/2) , (int)abs(($Y[$i-1]-$Y[$i])/2) );
if($m2<$m)
$m=$m2;
}
return $m;
}
User test case 1:
[[71, 88, 9, 13, 50, 67, 83, 7, 30, 92, 67, 92, 14, 16, 16, 13, 93, 52, 34, 97, 40, 69, 30, 6, 59, 85, 78, 18, 63, 95, 71, 80, 43, 31, 84, 31, 60, 16, 72, 61, 83, 35, 31, 36, 4, 100, 46, 21, 39, 61], [86, 87, 62, 80, 80, 0, 39, 66, 35, 6, 37, 53, 71, 70, 44, 33, 87, 78, 70, 94, 56, 29, 100, 65, 7, 14, 52, 95, 96, 37, 2, 96, 88, 47, 20, 97, 68, 74, 91, 31, 13, 52, 7, 70, 93, 25, 98, 10, 46, 13]]
Analysis
Code: 12:32:21 UTC,
php,
verify,
result: Passed
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$m2=floor(max(abs(($X[$i-1]-$X[$i])/2) , abs(($Y[$i-1]-$Y[$i])/2) ));
if($m2<$m)
$m=$m2;
}
return $m;
}
User test case 1:
[[71, 88, 9, 13, 50, 67, 83, 7, 30, 92, 67, 92, 14, 16, 16, 13, 93, 52, 34, 97, 40, 69, 30, 6, 59, 85, 78, 18, 63, 95, 71, 80, 43, 31, 84, 31, 60, 16, 72, 61, 83, 35, 31, 36, 4, 100, 46, 21, 39, 61], [86, 87, 62, 80, 80, 0, 39, 66, 35, 6, 37, 53, 71, 70, 44, 33, 87, 78, 70, 94, 56, 29, 100, 65, 7, 14, 52, 95, 96, 37, 2, 96, 88, 47, 20, 97, 68, 74, 91, 31, 13, 52, 7, 70, 93, 25, 98, 10, 46, 13]]
Analysis
expand all
User tests
1.
0.004 s
RUNTIME ERROR,
tested program terminated with exit code 1
stderr:
Invalid result type, int expected (got double)
Code: 12:32:55 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$m2=(infloor(max(abs(($X[$i-1]-$X[$i])/2) , abs(($Y[$i-1]-$Y[$i])/2) ));
if($m2<$m)
$m=$m2;
}
return $m;
}
Code: 12:32:57 UTC,
php,
verify,
result: Passed
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$m2=(int)floor(max(abs(($X[$i-1]-$X[$i])/2) , abs(($Y[$i-1]-$Y[$i])/2) ));
if($m2<$m)
$m=$m2;
}
return $m;
}
User test case 1:
[[71, 88, 9, 13, 50, 67, 83, 7, 30, 92, 67, 92, 14, 16, 16, 13, 93, 52, 34, 97, 40, 69, 30, 6, 59, 85, 78, 18, 63, 95, 71, 80, 43, 31, 84, 31, 60, 16, 72, 61, 83, 35, 31, 36, 4, 100, 46, 21, 39, 61], [86, 87, 62, 80, 80, 0, 39, 66, 35, 6, 37, 53, 71, 70, 44, 33, 87, 78, 70, 94, 56, 29, 100, 65, 7, 14, 52, 95, 96, 37, 2, 96, 88, 47, 20, 97, 68, 74, 91, 31, 13, 52, 7, 70, 93, 25, 98, 10, 46, 13]]
Analysis
Code: 12:33:39 UTC,
php,
autosave
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$m2=(int)(max(abs(($X[$i-1]-$X[$i])/2) , abs(($Y[$i-1]-$Y[$i])/2) ));
if($m2<$m)
$m=$m2;
}
return $m;
}
Code: 12:34:00 UTC,
php,
autosave
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$ii=$D[$i][0];
$m2=(int)max(abs(($X[$ii-1]-$X[$i])/2) , abs(($Y[$i-1]-$Y[$i])/2) );
if($m2<$m)
$m=$m2;
}
return $m;
}
Code: 12:34:14 UTC,
php,
verify,
result: Passed
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$ii=$D[$i][0];
$m2=(int)max(abs(($X[$ii-1]-$X[$ii])/2) , abs(($Y[$ii-1]-$Y[$ii])/2) );
if($m2<$m)
$m=$m2;
}
return $m;
}
User test case 1:
[[71, 88, 9, 13, 50, 67, 83, 7, 30, 92, 67, 92, 14, 16, 16, 13, 93, 52, 34, 97, 40, 69, 30, 6, 59, 85, 78, 18, 63, 95, 71, 80, 43, 31, 84, 31, 60, 16, 72, 61, 83, 35, 31, 36, 4, 100, 46, 21, 39, 61], [86, 87, 62, 80, 80, 0, 39, 66, 35, 6, 37, 53, 71, 70, 44, 33, 87, 78, 70, 94, 56, 29, 100, 65, 7, 14, 52, 95, 96, 37, 2, 96, 88, 47, 20, 97, 68, 74, 91, 31, 13, 52, 7, 70, 93, 25, 98, 10, 46, 13]]
Analysis
expand all
User tests
1.
0.004 s
OK
function result: 1
function result: 1
stderr:
PHP Notice: Undefined offset: -1 in func.php on line 67 Notice: Undefined offset: -1 in func.php on line 67 PHP Notice: Undefined offset: -1 in func.php on line 67 Notice: Undefined offset: -1 in func.php on line 67
Code: 12:35:20 UTC,
php,
autosave
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$ii=$D[$i][0];
$ii=$D[$i][0];
$m2=(int)max(abs(($X[$ii-1]-$X[$ii])/2) , abs(($Y[$ii-1]-$Y[$ii])/2) );
if($m2<$m)
$m=$m2;
}
return $m;
}
Code: 12:35:36 UTC,
php,
verify,
result: Passed
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$ii=$D[$i][0];
$ii2=$D[$i-1][0];
$m2=(int)max(abs(($X[$ii]-$X[$ii2])/2) , abs(($Y[$ii2]-$Y[$ii])/2) );
if($m2<$m)
$m=$m2;
}
return $m;
}
User test case 1:
[[71, 88, 9, 13, 50, 67, 83, 7, 30, 92, 67, 92, 14, 16, 16, 13, 93, 52, 34, 97, 40, 69, 30, 6, 59, 85, 78, 18, 63, 95, 71, 80, 43, 31, 84, 31, 60, 16, 72, 61, 83, 35, 31, 36, 4, 100, 46, 21, 39, 61], [86, 87, 62, 80, 80, 0, 39, 66, 35, 6, 37, 53, 71, 70, 44, 33, 87, 78, 70, 94, 56, 29, 100, 65, 7, 14, 52, 95, 96, 37, 2, 96, 88, 47, 20, 97, 68, 74, 91, 31, 13, 52, 7, 70, 93, 25, 98, 10, 46, 13]]
Analysis
Code: 12:35:45 UTC,
php,
verify,
result: Passed
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$ii=$D[$i][0];
$ii2=$D[$i-1][0];
$m2=(int)max(abs(($X[$ii]-$X[$ii2])/2) , abs(($Y[$ii2]-$Y[$ii])/2) );
if($m2<$m)
$m=$m2;
}
return $m;
}
User test case 1:
[[71, 88, 9, 13, 50, 67, 83, 7, 30, 92, 67, 92, 14, 16, 16, 13, 93, 52, 34, 97, 40, 69, 30, 6, 59, 85, 78, 18, 63, 95, 71, 80, 43, 31, 84, 31, 60, 16, 72, 61, 83, 35, 31, 36, 4, 100, 46, 21, 39, 61], [86, 87, 62, 80, 80, 0, 39, 66, 35, 6, 37, 53, 71, 70, 44, 33, 87, 78, 70, 94, 56, 29, 100, 65, 7, 14, 52, 95, 96, 37, 2, 96, 88, 47, 20, 97, 68, 74, 91, 31, 13, 52, 7, 70, 93, 25, 98, 10, 46, 13]]
Analysis
Code: 12:35:47 UTC,
php,
final,
score:
100
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475
// you can write to stdout for debugging purposes, e.g.
// print "this is a debug message\n";
function quick_sort($D, $s, $e)
{
//echo $s." ".$e."\n";
if($s == $e)
return array($D[$s]);
$m=(int)(($e-$s)/2);
$D1=quick_sort($D, $s, $s+$m);
$D2=quick_sort($D, $s+$m+1, $e);
$ret=array();
$l1=0;
$l2=0;
while($l1 < sizeof($D1) && $l2<sizeof($D2))
{
if($D1[$l1][1] <= $D2[$l2][1])
{
$ret[]=$D1[$l1];
$l1++;
continue;
}
if($D2[$l2][1] < $D1[$l1][1])
{
$ret[]=$D2[$l2];
$l2++;
continue;
}
}
while($l1<sizeof($D1))
$ret[]=$D1[$l1++];
while($l2<sizeof($D2))
$ret[]=$D2[$l2++];
return $ret;
}
function solution($X, $Y) {
//echo implode(",",$X)."\n";
//echo implode(",",$Y)."\n";
$D=array();
foreach($X as $i => $x)
{
$y=$Y[$i];
$D[]=array($i,sqrt($x*$x+$y*$y));
}
$D=quick_sort($D,0, sizeof($D)-1);
$i0=$D[0][0];
$i1=$D[1][0];
//echo $X[$i0].",".$Y[$i0]." ".$X[$i1].",".$Y[$i1]."\n";
$m=(int)max(abs(($X[$i0]-$X[$i1])/2) , abs(($Y[$i0]-$Y[$i1])/2) );
for($i=2;$i<sizeof($D);$i++)
{
$ii=$D[$i][0];
$ii2=$D[$i-1][0];
$m2=(int)max(abs(($X[$ii]-$X[$ii2])/2) , abs(($Y[$ii2]-$Y[$ii])/2) );
if($m2<$m)
$m=$m2;
}
return $m;
}Analysis summary
The solution obtained perfect score.
Analysis
Detected time complexity:
O(N*log(N))
expand all
Correctness tests
1.
0.004 s
OK
2.
0.004 s
OK
3.
0.004 s
OK
1.
0.004 s
OK
2.
0.004 s
OK
1.
0.008 s
OK
2.
0.008 s
OK
1.
0.008 s
OK
2.
0.004 s
OK
1.
0.004 s
OK
2.
0.008 s
OK
1.
0.008 s
OK
expand all
Performance tests
1.
0.004 s
OK
2.
0.004 s
OK
3.
0.004 s
OK
4.
0.004 s
OK
5.
0.004 s
OK
1.
0.768 s
OK
1.
0.276 s
OK
2.
0.100 s
OK
1.
0.008 s
OK
2.
0.680 s
OK
1.
0.276 s
OK
2.
0.060 s
OK
3.
0.016 s
OK
1.
0.660 s
OK