There are N ropes numbered from 0 to N − 1, whose lengths are given in an array A, lying on the floor in a line. For each I (0 ≤ I < N), the length of rope I on the line is A[I].
We say that two ropes I and I + 1 are adjacent. Two adjacent ropes can be tied together with a knot, and the length of the tied rope is the sum of lengths of both ropes. The resulting new rope can then be tied again.
For a given integer K, the goal is to tie the ropes in such a way that the number of ropes whose length is greater than or equal to K is maximal.
For example, consider K = 4 and array A such that:
A[0] = 1 A[1] = 2 A[2] = 3 A[3] = 4 A[4] = 1 A[5] = 1 A[6] = 3The ropes are shown in the figure below.

We can tie:
- rope 1 with rope 2 to produce a rope of length A[1] + A[2] = 5;
- rope 4 with rope 5 with rope 6 to produce a rope of length A[4] + A[5] + A[6] = 5.
After that, there will be three ropes whose lengths are greater than or equal to K = 4. It is not possible to produce four such ropes.
Write a function:
int solution(int K, vector<int> &A);
that, given an integer K and a non-empty array A of N integers, returns the maximum number of ropes of length greater than or equal to K that can be created.
For example, given K = 4 and array A such that:
A[0] = 1 A[1] = 2 A[2] = 3 A[3] = 4 A[4] = 1 A[5] = 1 A[6] = 3the function should return 3, as explained above.
Write an efficient algorithm for the following assumptions:
- N is an integer within the range [1..100,000];
- K is an integer within the range [1..1,000,000,000];
- each element of array A is an integer within the range [1..1,000,000,000].
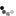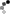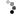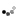 The submission is being evaluated.
The submission is being evaluated.