Test results - Codility

Tasks Details

medium

1. NumberOfDiscIntersections

Compute the number of intersections in a sequence of discs.

100%

We draw N discs on a plane. The discs are numbered from 0 to N − 1. An array A of N non-negative integers, specifying the radiuses of the discs, is given. The J-th disc is drawn with its center at (J, 0) and radius A[J].

We say that the J-th disc and K-th disc intersect if J ≠ K and the J-th and K-th discs have at least one common point (assuming that the discs contain their borders).

The figure below shows discs drawn for N = 6 and A as follows:

A[0] = 1 A[1] = 5 A[2] = 2 A[3] = 1 A[4] = 4 A[5] = 0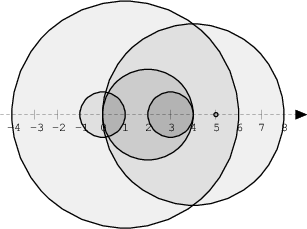

There are eleven (unordered) pairs of discs that intersect, namely:

discs 1 and 4 intersect, and both intersect with all the other discs;

disc 2 also intersects with discs 0 and 3.

Write a function:

function solution(A);

that, given an array A describing N discs as explained above, returns the number of (unordered) pairs of intersecting discs. The function should return −1 if the number of intersecting pairs exceeds 10,000,000.

Given array A shown above, the function should return 11, as explained above.

Write an efficient algorithm for the following assumptions:

N is an integer within the range [0..100,000];

each element of array A is an integer within the range [0..2,147,483,647].

Solution

Programming language used JavaScript

Time spent on task 3 minutes

Notes

not defined yet

Task timeline

Code: 11:17:15 UTC, js, verify, result: Passed

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44

// you can write to stdout for debugging purposes, e.g.
// console.log('this is a debug message');

function sortAsc(a, b) {
    return (a - b)
   }
   
   function solution(A) {
     let counter = 0
     let j= 0;
     let leftLimit = [];
     let rightLimit = []
   
     //fill the left and right limits of each circle
     for(var i=0; i < A.length; i++) {
      leftLimit[i] =i-A[i];
      rightLimit[i] =i+A[i];
     } 
     console.log(leftLimit)
     console.log(rightLimit)
   
     //sort them in an ascending order - why ? Basically we will rearrange their limits in an ascending way, we will have in leftLimit all open circles while  in the right we will have where the next circle closes
     leftLimit.sort(sortAsc)
     rightLimit.sort(sortAsc)
     console.log(leftLimit)
     console.log(rightLimit)

     //loop through all the elements of the RIGHT boundaries
     for(var i= 0; i<A.length; i++) {
      //this is the tricky part to understand
      //on the left we have the boundaries of open circles, on the right the boundary of the next circle
      //as long as there are circles open (rightLimit[i] >= leftLimit[j]) and (j < A.length)
      while(j < A.length && rightLimit[i] >= leftLimit[j]){
       //we have circles at each position, so, as long as the left boundaries are smaller or equal to the right boundary, there are circles intersecting there 
       //if j surpasses j, it means we overcalculated and we start to decrease the number of intersections   
       counter += j-i;
       //pass to the next open circle
       j++; 
      } 
        if(counter > 10000000) return -1;
     } 
   
     return counter;
   }

Analysis

▶

example1
example test

✔

Code: 11:17:23 UTC, js, autosave

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43

// you can write to stdout for debugging purposes, e.g.
// console.log('this is a debug message');

function sortAsc(a, b) {
    return (a - b)
   }
   
   function solution(A) {
     let counter = 0
     let j= 0;
     let leftLimit = [];
     let rightLimit = []
   
     //fill the left and right limits of each circle
     for(var i=0; i < A.length; i++) {
      leftLimit[i] =i-A[i];
      rightLimit[i] =i+A[i];
     } 
     console.log(rightLimit)
   
     //sort them in an ascending order - why ? Basically we will rearrange their limits in an ascending way, we will have in leftLimit all open circles while  in the right we will have where the next circle closes
     leftLimit.sort(sortAsc)
     rightLimit.sort(sortAsc)
     console.log(leftLimit)
     console.log(rightLimit)

     //loop through all the elements of the RIGHT boundaries
     for(var i= 0; i<A.length; i++) {
      //this is the tricky part to understand
      //on the left we have the boundaries of open circles, on the right the boundary of the next circle
      //as long as there are circles open (rightLimit[i] >= leftLimit[j]) and (j < A.length)
      while(j < A.length && rightLimit[i] >= leftLimit[j]){
       //we have circles at each position, so, as long as the left boundaries are smaller or equal to the right boundary, there are circles intersecting there 
       //if j surpasses j, it means we overcalculated and we start to decrease the number of intersections   
       counter += j-i;
       //pass to the next open circle
       j++; 
      } 
        if(counter > 10000000) return -1;
     } 
   
     return counter;
   }

Code: 11:17:28 UTC, js, verify, result: Passed

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

// you can write to stdout for debugging purposes, e.g.
// console.log('this is a debug message');

function sortAsc(a, b) {
    return (a - b)
   }
   
   function solution(A) {
     let counter = 0
     let j= 0;
     let leftLimit = [];
     let rightLimit = []
   
     //fill the left and right limits of each circle
     for(var i=0; i < A.length; i++) {
      leftLimit[i] =i-A[i];
      rightLimit[i] =i+A[i];
     } 

     //sort them in an ascending order - why ? Basically we will rearrange their limits in an ascending way, we will have in leftLimit all open circles while  in the right we will have where the next circle closes
     leftLimit.sort(sortAsc)
     rightLimit.sort(sortAsc)

     //loop through all the elements of the RIGHT boundaries
     for(var i= 0; i<A.length; i++) {
      //this is the tricky part to understand
      //on the left we have the boundaries of open circles, on the right the boundary of the next circle
      //as long as there are circles open (rightLimit[i] >= leftLimit[j]) and (j < A.length)
      while(j < A.length && rightLimit[i] >= leftLimit[j]){
       //we have circles at each position, so, as long as the left boundaries are smaller or equal to the right boundary, there are circles intersecting there 
       //if j surpasses j, it means we overcalculated and we start to decrease the number of intersections   
       counter += j-i;
       //pass to the next open circle
       j++; 
      } 
        if(counter > 10000000) return -1;
     } 
   
     return counter;
   }

Analysis

▶

example1
example test

✔

Code: 11:17:38 UTC, js, verify, result: Passed

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

// you can write to stdout for debugging purposes, e.g.
// console.log('this is a debug message');

function sortAsc(a, b) {
    return (a - b)
   }
   
   function solution(A) {
     let counter = 0
     let j= 0;
     let leftLimit = [];
     let rightLimit = []
   
     //fill the left and right limits of each circle
     for(var i=0; i < A.length; i++) {
      leftLimit[i] =i-A[i];
      rightLimit[i] =i+A[i];
     } 

     //sort them in an ascending order - why ? Basically we will rearrange their limits in an ascending way, we will have in leftLimit all open circles while  in the right we will have where the next circle closes
     leftLimit.sort(sortAsc)
     rightLimit.sort(sortAsc)

     //loop through all the elements of the RIGHT boundaries
     for(var i= 0; i<A.length; i++) {
      //this is the tricky part to understand
      //on the left we have the boundaries of open circles, on the right the boundary of the next circle
      //as long as there are circles open (rightLimit[i] >= leftLimit[j]) and (j < A.length)
      while(j < A.length && rightLimit[i] >= leftLimit[j]){
       //we have circles at each position, so, as long as the left boundaries are smaller or equal to the right boundary, there are circles intersecting there 
       //if j surpasses j, it means we overcalculated and we start to decrease the number of intersections   
       counter += j-i;
       //pass to the next open circle
       j++; 
      } 
        if(counter > 10000000) return -1;
     } 
   
     return counter;
   }

Analysis

▶

example1
example test

✔

Code: 11:17:42 UTC, js, final, score: 100

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

// you can write to stdout for debugging purposes, e.g.
// console.log('this is a debug message');

function sortAsc(a, b) {
    return (a - b)
   }
   
   function solution(A) {
     let counter = 0
     let j= 0;
     let leftLimit = [];
     let rightLimit = []
   
     //fill the left and right limits of each circle
     for(var i=0; i < A.length; i++) {
      leftLimit[i] =i-A[i];
      rightLimit[i] =i+A[i];
     } 

     //sort them in an ascending order - why ? Basically we will rearrange their limits in an ascending way, we will have in leftLimit all open circles while  in the right we will have where the next circle closes
     leftLimit.sort(sortAsc)
     rightLimit.sort(sortAsc)

     //loop through all the elements of the RIGHT boundaries
     for(var i= 0; i<A.length; i++) {
      //this is the tricky part to understand
      //on the left we have the boundaries of open circles, on the right the boundary of the next circle
      //as long as there are circles open (rightLimit[i] >= leftLimit[j]) and (j < A.length)
      while(j < A.length && rightLimit[i] >= leftLimit[j]){
       //we have circles at each position, so, as long as the left boundaries are smaller or equal to the right boundary, there are circles intersecting there 
       //if j surpasses j, it means we overcalculated and we start to decrease the number of intersections   
       counter += j-i;
       //pass to the next open circle
       j++; 
      } 
        if(counter > 10000000) return -1;
     } 
   
     return counter;
   }

Analysis summary

The solution obtained perfect score.

Analysis

Detected time complexity:

O(N*log(N)) or O(N)

▶

example1
example test

✔

▶

simple1

✔

▶

simple2

✔

▶

simple3

✔

▶

extreme_small
empty and [10]

✔

▶

small1

✔

▶

small2

✔

▶

small3

✔

▶

overflow
arithmetic overflow tests

✔

▶

medium1

✔

▶

medium2

✔

▶

medium3

✔

▶

medium4

✔

▶

10M_intersections
10.000.000 intersections

✔

▶

big1

✔

▶

big2

✔

▶

big3
[0]*100.000

✔