Tasks Details
medium
Compute the number of intersections in a sequence of discs.
Task Score
75%
Correctness
100%
Performance
50%
We draw N discs on a plane. The discs are numbered from 0 to N − 1. An array A of N non-negative integers, specifying the radiuses of the discs, is given. The J-th disc is drawn with its center at (J, 0) and radius A[J].
We say that the J-th disc and K-th disc intersect if J ≠ K and the J-th and K-th discs have at least one common point (assuming that the discs contain their borders).
The figure below shows discs drawn for N = 6 and A as follows:
A[0] = 1 A[1] = 5 A[2] = 2 A[3] = 1 A[4] = 4 A[5] = 0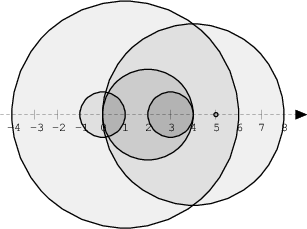
There are eleven (unordered) pairs of discs that intersect, namely:
- discs 1 and 4 intersect, and both intersect with all the other discs;
- disc 2 also intersects with discs 0 and 3.
Write a function:
class Solution { public int solution(int[] A); }
that, given an array A describing N discs as explained above, returns the number of (unordered) pairs of intersecting discs. The function should return −1 if the number of intersecting pairs exceeds 10,000,000.
Given array A shown above, the function should return 11, as explained above.
Write an efficient algorithm for the following assumptions:
- N is an integer within the range [0..100,000];
- each element of array A is an integer within the range [0..2,147,483,647].
Copyright 2009–2024 by Codility Limited. All Rights Reserved. Unauthorized copying, publication or disclosure prohibited.
Solution
Programming language used Java 8
Time spent on task 1 minutes
Notes
not defined yet
Task timeline
Code: 12:26:17 UTC,
java,
autosave
Code: 12:26:21 UTC,
java,
autosave
import java.util.*;
// you can write to stdout for debugging purposes, e.g.
// System.out.println("this is a debug message");
class Solution {
static class Circle implements Comparable<Circle> {
long right;
long left;
Circle(int pos, int length){
right = (long)pos + (long)length;
left = (long)pos - (long)length;
}
@Override
public int compareTo(Circle circle) {
if(this.left > circle.left){
return 1;
} else if(this.left == circle.left){
return Long.compare(this.right, circle.right);
} else{
return -1;
}
}
}
public int solution(int[] A) {
int cnt = 0;
Circle[] circleList = new Circle[A.length];
for (int i = 0; i < A.length; i++) {
circleList[i] = (new Circle(i, A[i]));
}
Arrays.sort(circleList);
for (int i = 0; i < A.length; i++) {
for (int j = i+1; j < A.length; j++) {
if(circleList[i].right >= circleList[j].left){
cnt++;
}else{
break;
}
}
}
return cnt;
}
}
Code: 12:26:22 UTC,
java,
verify,
result: Passed
import java.util.*;
// you can write to stdout for debugging purposes, e.g.
// System.out.println("this is a debug message");
class Solution {
static class Circle implements Comparable<Circle> {
long right;
long left;
Circle(int pos, int length){
right = (long)pos + (long)length;
left = (long)pos - (long)length;
}
@Override
public int compareTo(Circle circle) {
if(this.left > circle.left){
return 1;
} else if(this.left == circle.left){
return Long.compare(this.right, circle.right);
} else{
return -1;
}
}
}
public int solution(int[] A) {
int cnt = 0;
Circle[] circleList = new Circle[A.length];
for (int i = 0; i < A.length; i++) {
circleList[i] = (new Circle(i, A[i]));
}
Arrays.sort(circleList);
for (int i = 0; i < A.length; i++) {
for (int j = i+1; j < A.length; j++) {
if(circleList[i].right >= circleList[j].left){
cnt++;
}else{
break;
}
}
}
return cnt;
}
}
Analysis
Code: 12:26:26 UTC,
java,
final,
score:
75
import java.util.*;
// you can write to stdout for debugging purposes, e.g.
// System.out.println("this is a debug message");
class Solution {
static class Circle implements Comparable<Circle> {
long right;
long left;
Circle(int pos, int length){
right = (long)pos + (long)length;
left = (long)pos - (long)length;
}
@Override
public int compareTo(Circle circle) {
if(this.left > circle.left){
return 1;
} else if(this.left == circle.left){
return Long.compare(this.right, circle.right);
} else{
return -1;
}
}
}
public int solution(int[] A) {
int cnt = 0;
Circle[] circleList = new Circle[A.length];
for (int i = 0; i < A.length; i++) {
circleList[i] = (new Circle(i, A[i]));
}
Arrays.sort(circleList);
for (int i = 0; i < A.length; i++) {
for (int j = i+1; j < A.length; j++) {
if(circleList[i].right >= circleList[j].left){
cnt++;
}else{
break;
}
}
}
return cnt;
}
}Analysis summary
The following issues have been detected: timeout errors.
Analysis
Detected time complexity:
O(N**2)
expand all
Correctness tests
1.
0.004 s
OK
1.
0.004 s
OK
2.
0.004 s
OK
1.
0.004 s
OK
1.
0.008 s
OK
2.
0.004 s
OK
1.
0.004 s
OK
1.
0.004 s
OK
1.
0.004 s
OK
1.
0.004 s
OK
2.
0.004 s
OK
expand all
Performance tests
1.
0.020 s
OK
1.
0.052 s
OK
1.
0.076 s
OK
1.
0.252 s
TIMEOUT ERROR,
running time: 0.252 sec., time limit: 0.128 sec.
10M_intersections
10.000.000 intersections
10.000.000 intersections
✘
TIMEOUT ERROR
running time: 0.244 sec., time limit: 0.100 sec.
running time: 0.244 sec., time limit: 0.100 sec.
1.
0.244 s
TIMEOUT ERROR,
running time: 0.244 sec., time limit: 0.100 sec.
1.
0.744 s
TIMEOUT ERROR,
running time: 0.744 sec., time limit: 0.560 sec.
2.
0.004 s
OK
1.
2.596 s
TIMEOUT ERROR,
running time: 2.596 sec., time limit: 1.104 sec.
2.
0.004 s
OK
1.
0.208 s
OK
2.
0.004 s
OK