Tasks Details
easy
1.
StoneWall
Cover "Manhattan skyline" using the minimum number of rectangles.
Task Score
100%
Correctness
100%
Performance
100%
You are going to build a stone wall. The wall should be straight and N meters long, and its thickness should be constant; however, it should have different heights in different places. The height of the wall is specified by an array H of N positive integers. H[I] is the height of the wall from I to I+1 meters to the right of its left end. In particular, H[0] is the height of the wall's left end and H[N−1] is the height of the wall's right end.
The wall should be built of cuboid stone blocks (that is, all sides of such blocks are rectangular). Your task is to compute the minimum number of blocks needed to build the wall.
Write a function:
function solution(H);
that, given an array H of N positive integers specifying the height of the wall, returns the minimum number of blocks needed to build it.
For example, given array H containing N = 9 integers:
H[0] = 8 H[1] = 8 H[2] = 5 H[3] = 7 H[4] = 9 H[5] = 8 H[6] = 7 H[7] = 4 H[8] = 8the function should return 7. The figure shows one possible arrangement of seven blocks.
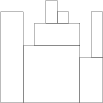
Write an efficient algorithm for the following assumptions:
- N is an integer within the range [1..100,000];
- each element of array H is an integer within the range [1..1,000,000,000].
Copyright 2009–2024 by Codility Limited. All Rights Reserved. Unauthorized copying, publication or disclosure prohibited.
Solution
Programming language used JavaScript
Time spent on task 2 minutes
Notes
not defined yet
Task timeline
Code: 07:58:02 UTC,
java,
autosave
Code: 07:58:15 UTC,
js,
autosave
// you can write to stdout for debugging purposes, e.g.
// console.log('this is a debug message');
function solution(H) {
const stack = []
let count = 0
for (let i=1; i<H.length; i++) {
// 베이스가 돌을 찾는다.
// 베이스가 될 돌은 무조건 하나 있어야 하고
// 현재 쌓으려는 돌 위치보다 낮아야 한다.
while (stack.length !== 0 && stack[stack.length-1] > H[i]) {
stack.pop()
}
// 돌 명단이 비어있거나, 새로 쌓아야 할 돌이 스택의 마지막 돌 보다 높다면 새로 쌓는다.
if (stack.length === 0 || stack[stack.length-1] < H[i]) {
// 새로 쌓고 지금 높이를 리턴한다.
stack.push(H[i])
count += 1
}
}
return count
}
Code: 07:58:38 UTC,
js,
autosave
// you can write to stdout for debugging purposes, e.g.
// console.log('this is a debug message');
function solution(H) {
const stack = []
let count = 0
for (let i=1; i<H.length; i++) {
// 베이스가 돌을 찾는다.
// 베이스가 될 돌은 무조건 하나 있어야 하고
// 현재 쌓으려는 돌 위치보다 낮아야 한다.
while (stack.length > 0 && stack[stack.length-1] > H[i]) {
stack.pop()
}
// 돌 명단이 비어있거나, 새로 쌓아야 할 돌이 스택의 마지막 돌 보다 높다면 새로 쌓는다.
if (stack.length === 0 || stack[stack.length-1] < H[i]) {
// 새로 쌓고 지금 높이를 리턴한다.
stack.push(H[i])
count += 1
}
}
return count
}
Code: 07:59:00 UTC,
js,
autosave
// you can write to stdout for debugging purposes, e.g.
// console.log('this is a debug message');
function solution(H) {
const stack = []
let count = 0
for (let i=0; i<H.length; i++) {
// 베이스가 돌을 찾는다.
// 베이스가 될 돌은 무조건 하나 있어야 하고
// 현재 쌓으려는 돌 위치보다 낮아야 한다.
while (stack.length > 0 && stack[stack.length-1] > H[i]) {
stack.pop()
}
// 돌 명단이 비어있거나, 새로 쌓아야 할 돌이 스택의 마지막 돌 보다 높다면 새로 쌓는다.
if (stack.length === 0 || stack[stack.length-1] < H[i]) {
// 새로 쌓고 지금 높이를 리턴한다.
stack.push(H[i])
count += 1
}
}
return count
}
Code: 07:59:04 UTC,
js,
verify,
result: Passed
// you can write to stdout for debugging purposes, e.g.
// console.log('this is a debug message');
function solution(H) {
const stack = []
let count = 0
for (let i=0; i<H.length; i++) {
// 베이스가 돌을 찾는다.
// 베이스가 될 돌은 무조건 하나 있어야 하고
// 현재 쌓으려는 돌 위치보다 낮아야 한다.
while (stack.length > 0 && stack[stack.length-1] > H[i]) {
stack.pop()
}
// 돌 명단이 비어있거나, 새로 쌓아야 할 돌이 스택의 마지막 돌 보다 높다면 새로 쌓는다.
if (stack.length === 0 || stack[stack.length-1] < H[i]) {
// 새로 쌓고 지금 높이를 리턴한다.
stack.push(H[i])
count += 1
}
}
return count
}
Analysis
Code: 07:59:13 UTC,
js,
verify,
result: Passed
// you can write to stdout for debugging purposes, e.g.
// console.log('this is a debug message');
function solution(H) {
const stack = []
let count = 0
for (let i=0; i<H.length; i++) {
// 베이스가 돌을 찾는다.
// 베이스가 될 돌은 무조건 하나 있어야 하고
// 현재 쌓으려는 돌 위치보다 낮아야 한다.
while (stack.length > 0 && stack[stack.length-1] > H[i]) {
stack.pop()
}
// 돌 명단이 비어있거나, 새로 쌓아야 할 돌이 스택의 마지막 돌 보다 높다면 새로 쌓는다.
if (stack.length === 0 || stack[stack.length-1] < H[i]) {
// 새로 쌓고 지금 높이를 리턴한다.
stack.push(H[i])
count += 1
}
}
return count
}
Analysis
Code: 07:59:16 UTC,
js,
final,
score:
100
// you can write to stdout for debugging purposes, e.g.
// console.log('this is a debug message');
function solution(H) {
const stack = []
let count = 0
for (let i=0; i<H.length; i++) {
// 베이스가 돌을 찾는다.
// 베이스가 될 돌은 무조건 하나 있어야 하고
// 현재 쌓으려는 돌 위치보다 낮아야 한다.
while (stack.length > 0 && stack[stack.length-1] > H[i]) {
stack.pop()
}
// 돌 명단이 비어있거나, 새로 쌓아야 할 돌이 스택의 마지막 돌 보다 높다면 새로 쌓는다.
if (stack.length === 0 || stack[stack.length-1] < H[i]) {
// 새로 쌓고 지금 높이를 리턴한다.
stack.push(H[i])
count += 1
}
}
return count
}Analysis summary
The solution obtained perfect score.
Analysis
Detected time complexity:
O(N)
expand all
Correctness tests
1.
0.068 s
OK
1.
0.068 s
OK
1.
0.068 s
OK
1.
0.068 s
OK
2.
0.068 s
OK
1.
0.068 s
OK
2.
0.068 s
OK
3.
0.068 s
OK
4.
0.068 s
OK
expand all
Performance tests
1.
0.068 s
OK
1.
0.068 s
OK
1.
0.068 s
OK
1.
0.068 s
OK
1.
0.112 s
OK
1.
0.108 s
OK
2.
0.108 s
OK
1.
0.104 s
OK
1.
0.104 s
OK
1.
0.112 s
OK